W artykule o sztucznym horyzoncie powiedzieliśmy o podstawowym problemie określania orientacji w przestrzeni z wykorzystaniem żyroskopu. Chodzi tu o ciągłe utrzymywanie jego płaszczyzny wirowania prostopadle do pionu lokalnego. Problem rozwiązuje nawigacja bezkardanowa, niewymagająca specjalnego zawieszenia żyroskopu.
Całość składa się z czujników prędkości kątowych (elektronicznych żyroskopów) i przyspieszeniomierzy (również elektronicznych), umieszczonych na trzech prostopadłych osiach oraz z komputera. Elementy pomiarowe wraz z procesorem (komputerem) są sztywno zamontowane na platformie, która z kolei przymocowana jest to statku powietrznego.
Widzimy, że w takim rozwiązaniu niemożliwe jest, aby prędkości kątowe mierzone były w układzie związanym z przestrzenią inercjalną, ponieważ są one przymocowane do samolotu. Całość wygląda następująco:
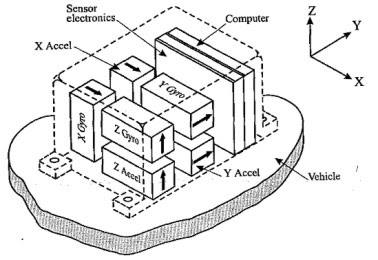 |
| Rys. 1 - Bezkardanowy system nawigacji [1] |
Bez zagłębiania się w algorytmy obliczania orientacji przestrzennej nie jesteśmy w stanie dokładnie opisać współdziałania żyroskopów i przyspieszeniomierzy. Ogólnie, rzecz polega na ciągłym pobieraniu danych z czujników (np. co 0,01 s), obliczaniu chwilowego położenia osi samolotu względem Ziemi przy użyciu macierzy transformacji, określania przyspieszeń na tych osiach i zliczaniu drogi. Dodatkowym sygnałem, używanym w obliczeniach, mogą być dane z magnetometru, czyli kurs.
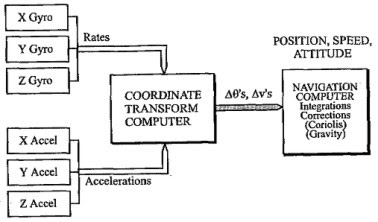 |
| Rys. 2 - Schemat obliczania orientacji przestrzennej [1] |
Sprawa wygląda całkiem banalnie, gdy samolot leci lotem ustalonym przez większość drogi i tylko czasami wykonuje manewry, powodujące powstawanie dodatkowych przyspieszeń. Problemy pojawiają się, gdy pilot długotrwale krąży lub ciągle wykonuje gwałtowne manewry, przechylenia itp. W tym przypadku należy dodatkowo korygować obliczenia.
 |
| Rys. 3 - Budowa systemu AHRS [2] |
Na powyższych zasadach działają systemy AHRS, określające orientację samolotu w przestrzeni. Rozwiązanie stosowane jest również w amatorskich autopilotach, tj. OpenPilot, ArduPilot i wielu innych. Dlatego praktycznie zawsze w ich specyfikacji podawana jest informacja o rodzajach zainstalowanych żyroskopów i przyspieszeniomierzy. Opcjonalnie może pojawić się też magnetometr.
Zalety i wady
Wiadomo, nie istnieją rozwiązania idealne. pProsta struktura, niski koszt budowy, niewielkie wymiary i waga, niezawodność, wytrzymałość - to są zalety systemów bezkardanowych. Nie należy zapominać do istnieniu błędów przyspieszeniomierzy, żyroskopów, wymaganiu kalibracji czujników oraz bardzo szybkiego komputera, który nadąży ze wszystkimi obliczeniami.
Źródła:
1. A. Lawrence: "Modern Inertial Technology"
2. http://www.hsfsolutions.com
